Geodetic Datums

Overview

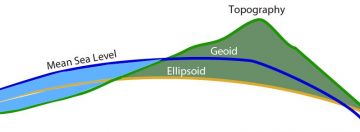
Geodetic datums provide a reference frame for three-dimensional positioning applications such as surveying, navigation, mapmaking and geographic information systems (GIS). They are based on two types of surfaces (Figure 1). The first surface, an oblate ellipsoid of revolution, is a purely mathematical construct that approximates the Earth’s size and shape and is used as a reference for geodetic latitude and longitude (Figure 1). The second surface, the geoid, is a physical (geopotential) surface defined by the gravity field, used as a reference for height above sea level.

The ellipsoid is uniquely defined by two parameters, the semimajor axis a and inverse flattening (1/f). These are supplemented by specification of the ellipsoid’s center, its orientation and scale, together which uniquely define a horizontal geodetic datum. The most recent global geodetic reference frame is WGS84 with semi-major axis a=6378137, and an inverse flattening 1/f=298.257 223 563. WGS84 is maintained by the U.S. Department of Defense (DoD) for GPS orbit determination and positioning. In space geodetic and geophysical applications, we use an Earth-Fixed, Earth-Centered reference frame (Figure 2) realized by the “Cartesian” (X, Y, Z) coordinates and their changes over time of a network of globally-distributed space geodetic tracking stations (GNSS/GPS, very long baseline interferometry, satellite laser ranging), at a particular epoch of time. The universally-recognized reference frame is the International Terrestrial Reference Frame (ITRF), which is updated every few years as more data are collected from a growing number of stations and as physical models are improved. The latest incarnation of ITRF is ITRF2014. WGS84 is kept consistent with the ITRF within a meter, worldwide. For more details see review by Bock and Melgar (2016) and references therein.

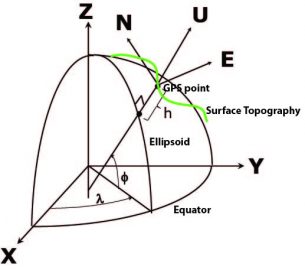
Coordinate Systems — Figure 2. Geodetic coordinate systems. Analysis of GPS phase and pseudorange data is carried out in ITRF coordinates. An alternate representation is geodetic latitude, longitude and height with respect to a geocentric oblate ellipsoid (one octant shown) aligned with the zero meridian (X-axis) and pole (Z-axis). (Bock and Melgar, 2016)

The relationship between geodetic coordinates (φ, λ, h), (latitude, longitude, ellipsoidal height), and ITRF (X, Y, Z) coordinates (Figure 2) is

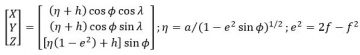
where e is ellipsoid’s eccentricity. The geodetic height (h) is the distance from a point on the Earth’s surface to the surface of the ellipsoid along the normal to the ellipsoid. It differs from the physical height H above the geoid along a direction defined by the local plumb line and the Earth’s gravity field. The geoid is the basis of a physical vertical datum. The difference between the physical height and geometric height is called the geoid undulation N, according to H = h – N. The ellipsoid deviates from the geoid globally by about -105 m to 85 m. Today, geodetic datums are defined by the latitudes and longitudes of GNSS stations (continuous or surveyed) given at a particular epoch of time (for the horizontal) and by a geoid model (for the vertical). Previously, datums were defined through triangulation, trilateration and astronomic measurements of latitude and longitude (for the horizontal), and spirit leveling for the vertical. The relationships between datums are given by mathematical transformations.

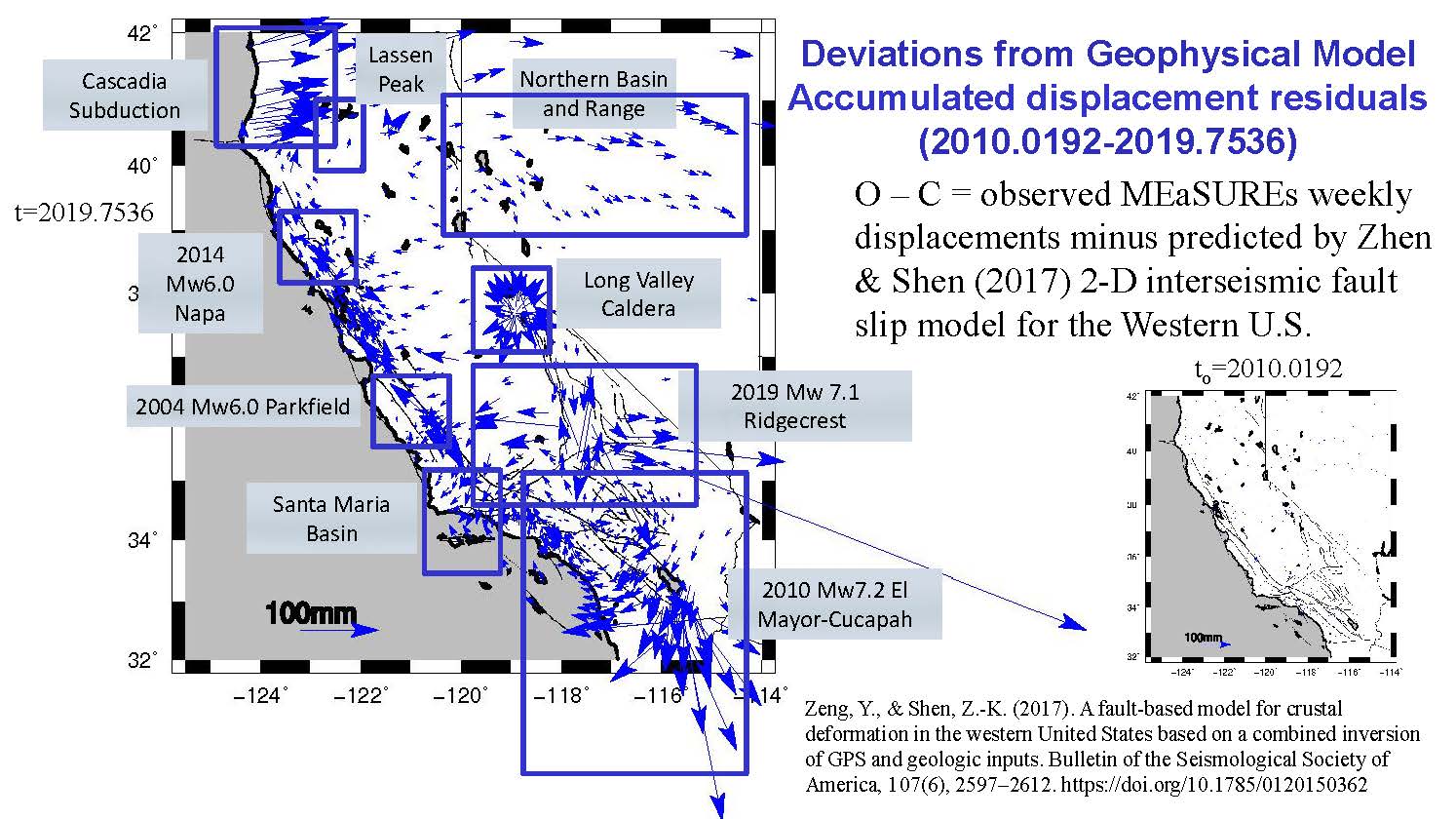
It is challenging to maintain a geodetic datum in the presence of crustal motion, including steady ("secular") motions and transient motions at various spatial and temporal scales (Figure 3). Our focus at SOPAC is California, which sits on the boundary of the North America and Pacific plates resulting in a steady, primarily horizontal motion on the order of up to 50 mm/yr on the San Andreas Fault System distributed over a width of hundreds of kilometers. North of Cape Mendocino, the tectonic regime changes from primarily strike slip motion to thrust faulting along the Cascadia Subduction Zone (Figure 3). This steady motion is punctuated by significant earthquakes that may instantaneously cause up to a meter of motion near the earthquake’s epicenter followed by significant postseismic motion over a period of months to years until the crust returns to its steady state. Since 1992, California has experienced twenty earthquakes from magnitudes 5.1-7.2 that significantly affected the positions of one to hundreds of stations. For example, the April 4, 2010 Mw 7.2 El Mayor-Cucapah earthquake in northern Baja California, Mexico caused significant coseismic motion (up to 0.3 meters) throughout southern California and an additional 50% cumulative postseismic motion over a period of nearly 10 years. Other transient motions are related to tectonic and magmatic processes and vertical land motion (subsidence and uplift) due to natural (e.g., drought) and/or anthropogenic (e.g., water and oil extraction) effects (Klein et al., 2019).

Figure 3. Shown are the accumulated residual horizontal displacements from the start of 2010 until mid-October, 2019 for California and Nevada (Klein et al., 2019) showing transients, as well as observed secular differences with the model of Zeng and Shen (2017). The weekly accumulation of the gridded displacement residuals forms the basis for defining a kinematic reference frame (Figures 5-6). We see significant secular differences with the model, for example, in Cascadia, the Northern Basin and Range, and the Santa Maria basin, that can then be used for improving secular fault slip models. Transients include postseismic motion for 4 earthquakes over these 10 years, and the horizontal expression of magmatic inflation at Long Valley Caldera and Lassen Peak (Bock et al., 2019).

The California Spatial Reference System Epoch 2017.50(NAD83)

The datum for California is the California Spatial Reference System (CSRS) realized through the positions of the continuous GPS (cGPS) stations that comprise the California Spatial Reference Network (CSRN). To minimize the deviations in station coordinates due to crustal and other motions (Figure 3), the CSRC has published updated geodetic datums every few years referred to as “Epoch Dates” at 2007.00 (based on 551 stations), 2009.00 (766 stations) and 2011.00 (830 stations). The latest one is Epoch 2017.50 commissioned by the California Department of Transportation (Caltrans) using nearly 948 cGPS stations (Figure 4). The new datum is fundamentally tied to the ITRF2014 through reanalysis of the raw GPS data and metadata collected at the CSRN cGPS stations from 1995 to September 30, 2017, and data from about 400 global tracking stations of the International GNSS Service (IGS). The ITRF2014 coordinates of the 948 stations are transformed into WGS84 geodetic coordinates: latitudes, longitude and ellipsoidal height (Figure 2). CSRS Epoch 2017.50(NAD83) is related to the current definition of the National Spatial Reference System (NSRS) through a set of coordinate transformations from ITRF2014 to NAD83(2011) published by the National Geodetic Survey, which is responsible for maintaining the geodetic datum for the U.S. and its territories. A complete description of this Epoch Date is given in a report to Caltrans, “California Spatial Reference System, CSRS Epoch 2017.50 (NAD83).”

Figure 4. California is subject to significant 3-D crustal motions which complicates the definition and maintenance of the geodetic reference frame. Current practice is to publish coordinates and velocities and their uncertainties for cGPS stations at a new Epoch Date every few years. (Bock et al., 2019).

In addition, geoid model GEOID12B published by NGS is used to interpolate geoid heights for each of the cGPS stations at 2017.50, thus providing access to a vertical datum for California.

Note that the NGS plans to replace NAD83 with a new geometric reference frame. The North American Terrestrial Reference Frame of 2022 (NATRF 2022) will be a “plate fixed” system, with the application of rotations about a Euler Pole to remain closely anchored to the North American tectonic plate.

Kinematic Datum

To illustrate the limitations of the Epoch Date approach, the July 4-6 2019 Ridgecrest earthquakes displaced about 150 CSRN stations in a radius of several hundred kms from their source. To compensate for the station movements, the CSRC published provisional Epoch Date 2019.55 for users of the affected stations.

Horizontal Datum

Caltrans contracted the CSRC to investigate the feasibility of defining and maintaining a “kinematic” datum for California that would replace the Epoch Date approach (Figure 5). The details and conclusions of this study are found in the report “Investigations into a Dynamic Datum for California.” The objective is to provide a utility for surveying and precise spatial referencing within an active tectonic area spanned by a dense cGPS reference network. This would allow for the transformation of coordinates from one date to another (Figure 6), without the need for periodic Epoch Date definitions, such as Epochs 2011.00 and 2017.50.

Figure 5. A secular model (Zeng and Shen, 2017) is used to construct a reference displacement grid, as well as a grid based on the observed displacement residuals between the observed displacements and the displacements predicted by the model. The two grids are then added together to produce a weekly horizontal displacement field (shown here for the east component). Each displacement grid is time tagged and archived. The summed grids define the kinematic reference frame at a particular epoch of time (Klein et al., 2019).

Figure 6. Concept of a kinematic datum. Transformation of station coordinates for two separate surveys to Epoch 2011.00, one with true-of-date RTK surveying (t3=2017.65) and one in post-processing (t2=2012.65). Best practices call for positioning with respect to the latest version of ITRF (ITRF2014), which is consistent with the GPS broadcast ephemerides and published ultra-precise and final IGS orbits. The dynamic datum allows the coordinates at t3 and t2 to be transformed to an arbitrary epoch t1, still in ITRF, using archived coordinate correction grids updated weekly at SOPAC. The coordinates can then be transformed to NAD83, or other datum of choice at t3 and t2. Epoch t2 refers to the start of the daily displacements time series (Klein et al., 2019).

Figure 7. Accumulated vertical displacement field between 1999.5 and 2018.6, represented with two different color scales to highlight significantly greater vertical motion in the Central Valley. Zones a-n with significant vertical motion are defined in Klein et al. (2019).

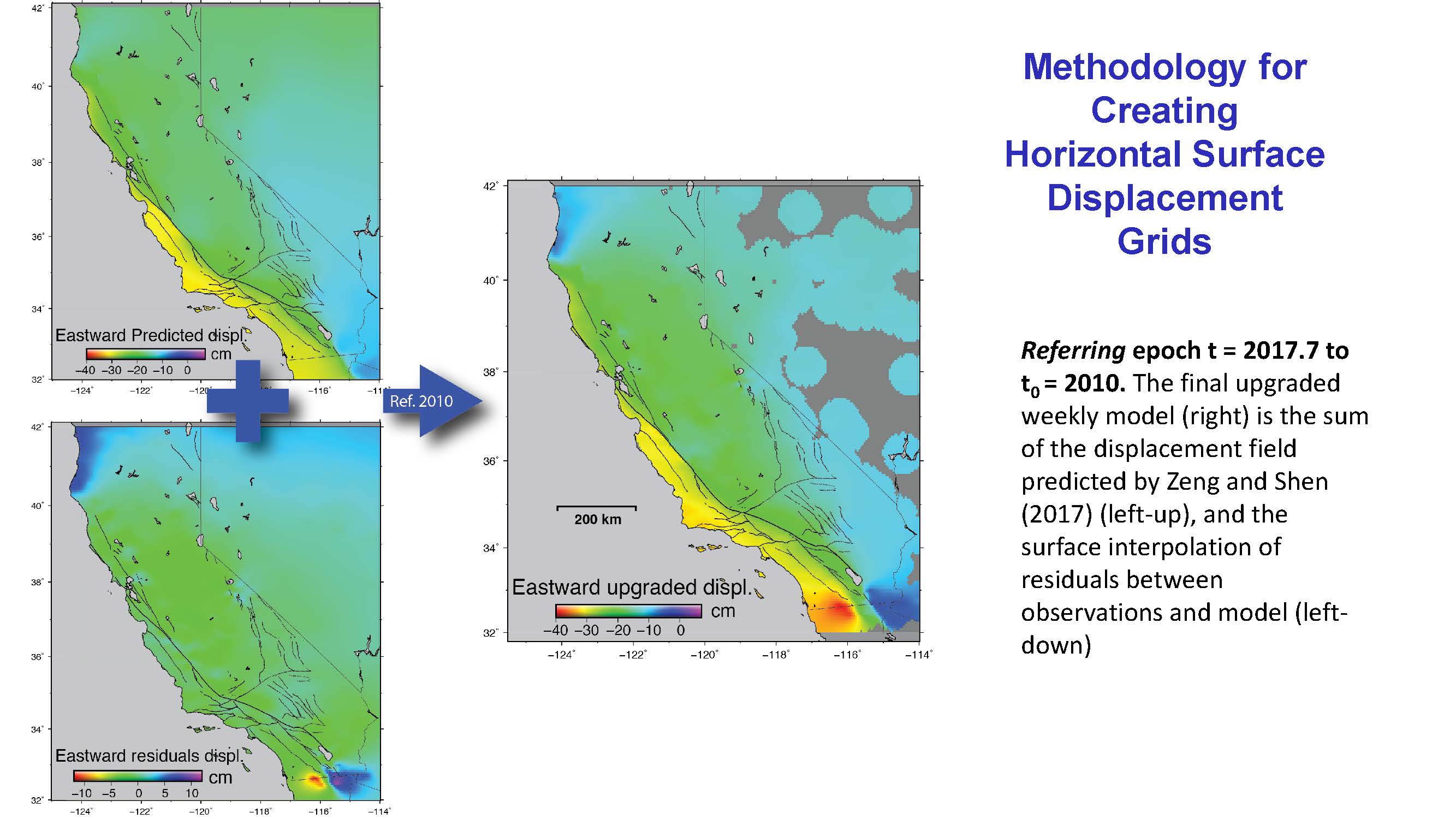
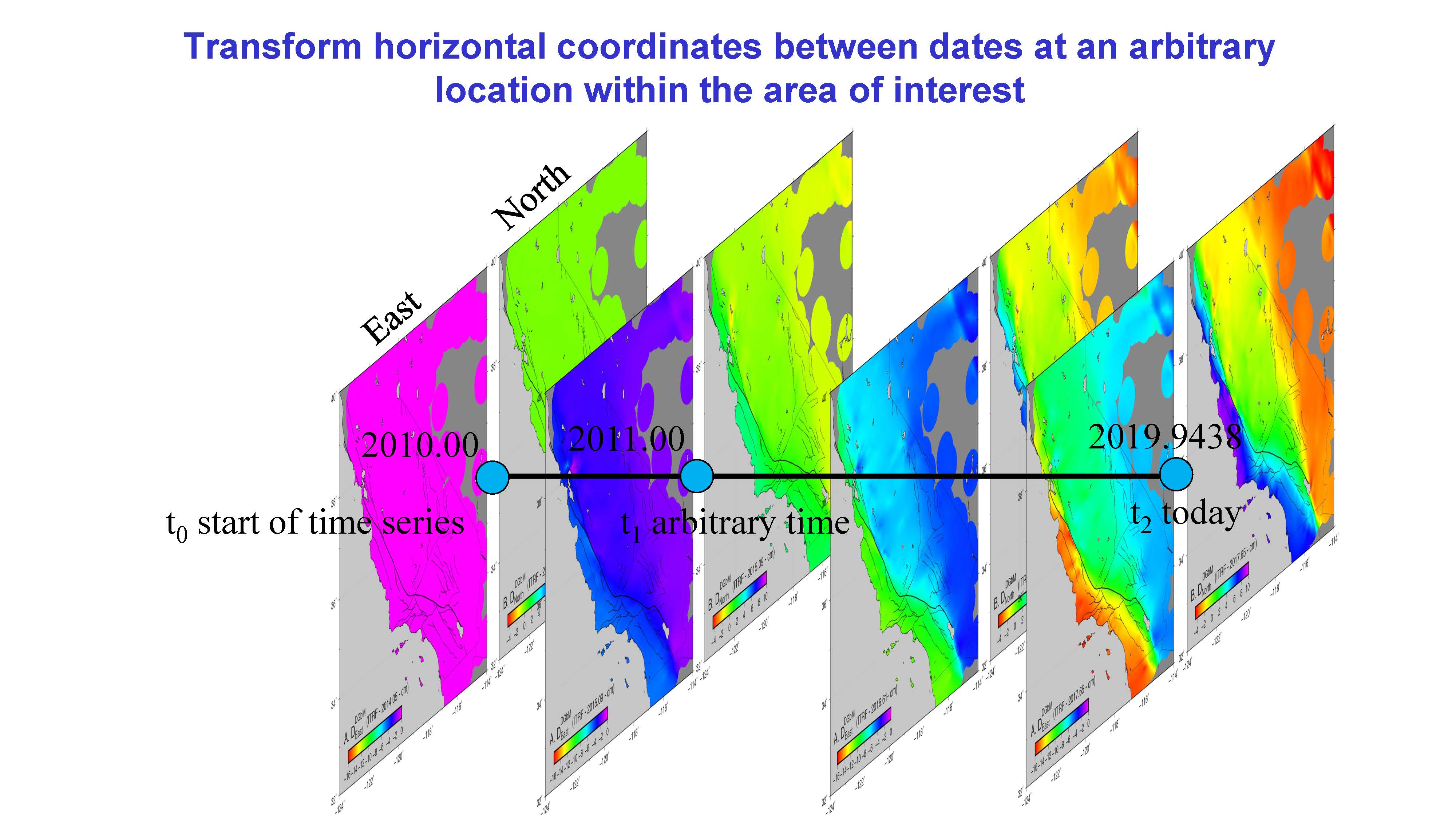
Vertical Datum

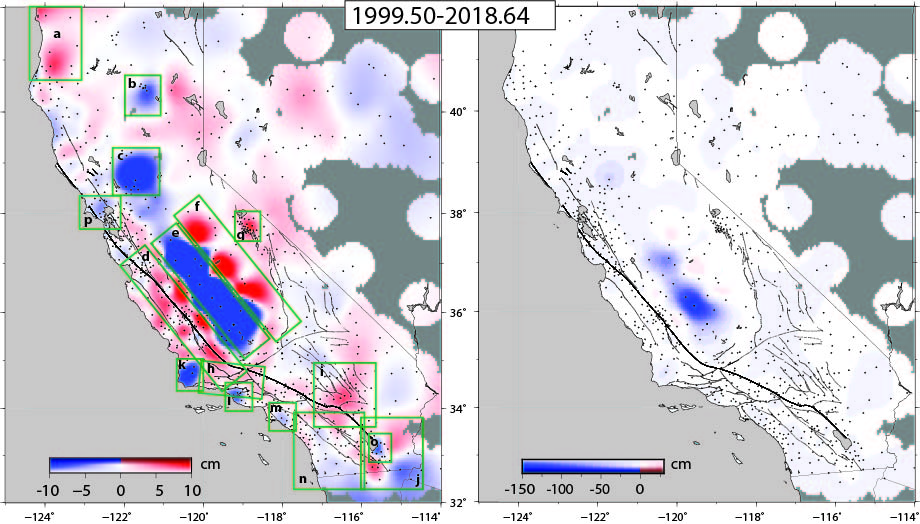
Vertical motions are considerably more erratic and, hence, difficult to model. For instance, vertical displacements in the Central Valley (Figure 7) display numerous changes in slope related to drought, land use, water policy, etc. They are related to natural sources (e.g., climate, hydrology, drought, water recharge), anthropogenic effects (e.g., water and mineral withdrawal, hydrothermal power), and magmatism, typically greater in magnitude than tectonic processes. The effects of tectonic processes result in smaller vertical displacements throughout California, except for the coastal regions of northern California along the Cascadia subduction zone. Therefore, we do not use a geophysical or other vertical model but simply interpolate the observed vertical displacements on a weekly basis (Figure 7).

Publications

Bock, Y. and D. Melgar (2016), Physical Applications of GPS Geodesy: A Review, Reports on Progress Physics, 79, 10, doi:10.1088/0034-4885/79/10/106801.

Bock, Y., P. Fang and G. R. Helmer (2018), California Spatial Reference System: CSRS Epoch 2017.50 (NAD83), Final report to California Department of Transportation (Caltrans), January 4.

Bock, Y. and E. Klein (2018), Investigations into a Dynamic Datum for California, Final report to California Department of Transportation (Caltrans), June 22.

Bock, Y., E. Klein, A. M. Moore, X. Xu, D. T. Sandwell, P. Fang, D. Golriz, D. Argus, Z. Liu, S. Kedar (2019), Kinematic Reference Frame for the Crustal Deformation Cycle: Transients and Model Discrepancies, Abstract G32A-06, presented at 2019 Fall Meeting, AGU, San Francisco., 9-13 Dec.

Klein, K., Y. Bock, X. Xu, D. Sandwell, D. Golriz, P. Fang, L. Su (2019), Transient deformation in California from two decades of GPS displacements: Implications for a three-dimensional kinematic reference frame, J. Geophys. Res., https://doi.org/10.1029/2018JB017201

Zeng, Y., and Shen, Z.‐K. (2017), A fault‐based model for crustal deformation in the western United States based on a combined inversion of GPS and geologic inputs. Bulletin of the Seismological Society of America, 107(6), 2597–2612. https://doi.org/10.1785/0120150362